Ilustração do ensino da geometria numa
tradução medieval de Os elementos de Euclides.
Tempo de leitura: 35 min.
Apresentamos, hoje a cópia de uma carta de Francisco Sanches a Cristóvão Clávio, publicada pelo P. Iriarte no Gregorianum (Revista da Universidade Gregoriana de Roma). É anônima ou, melhor, esconde o nome sob o pseudônimo de Carnéades. Mas não há dúvida ser ela de Sanches. Esta carta deve ter sido escrita, segundo nota o P. Iriarte, por volta dos anos de 1589-1590.
Esta carta também foi publicada em português na Revista Portuguesa de Filosofia, T. 1, Fasc. 3 (Jul. - Sep., 1945), pp. 294-305 e está disponível AQUI e TAMBÉM AQUI
***
Introdução
O talento, excepcionalmente dotado, de Francisco Sanches exercitou-se em quase todos os ramos do saber humano: nas letras e na poesia, logo nos primeiros anos da juventude, e de que ainda conservamos amostras no Carmen de Cometa; na filosofia e medicina, de que nos falam ainda, hoje, as suas principais obras, recolhidas pelo discípulo e admirador Raimundo Delassus; e na matemática. Já Delassus se refere à sua aplicação e gosto por esta última disciplina, e às dúvidas que lhe torturavam a alma, sedenta de luz plena da verdade. «Primus in stadio litterario labor eiusden in Mathematis enituit in quibus quid profecerit, maius non suppetit argumentum, quam obiectiones et ἐρωτήματα super geometricas Euclidis demonstrationes, quae a se primum excogitata, ad Clavium solvenda transmisit: fuit autem Clavius geometrarum rerum suo tempore decus, quibus Clavius satisfacere nititur perhonorifica responsione; sed frustra, ut idem Sanchez existimat, qui eas difficultates molitur in Theonem primarium Euclidis interpretem, et quae in mediis schedis repertae dum medica ipsius tanquam sybillae folia congererentur, iunctae fuissent medicis, nisi institutum operis repugnaret»! (Opera medica, introd. p. 3). Ficamos, pois, sabendo, por este depoimento de Delassus, que ele, ao reunir para a imprensa as obras do mestre, teve sob os olhos toda ou parte da correspondência entabulada entre Sanches e Clávio, e que não a incluiu na sua obra, por não se coadunar facilmente com o objetivo da mesma. E foi pena, porque nunca mais se soube do paradeiro dessa correspondência. Só, em 1940, o P. J. Iriarte — Ag., S. J., grande admirador de Sanches, conseguiu, revolvendo o fundo «Clávio» da Universidade Gregoriana, em Roma, encontrar uma dessas cartas-consultas de Sanches, carta publicada, ainda nesse ano, na conceituada revista dessa universidade, Gregorianum. Supõe, esta carta, uma troca de correspondência entre Sanches e Clávio, bastante ativa. Sanches escreveu, uma primeira vez, comunicando-lhe algumas dúvidas sobre Proclo. Clávio respondeu, e a amabilidade da resposta animou Sanches a dirigir-lhe segunda consulta. Fê-lo, e de novo insiste sobre as mesmas objeções contra Proclo, refutando, de passo, a resposta de Clávio. Não sabemos, se este correspondeu, ainda desta vez, ao apelo de Sanches: «Gratissimum feceris si rescripseris», ser-me-ia gratíssimo receber, de novo, carta vossa. Por fim, o testemunho de Delassus obriga-nos a admitir, pelo menos, uma terceira consulta, em que Sanches representava as suas dificuldades contra Téon, principal comentador de Euclides.
Apresentamos, hoje, aos nossos leitores a cópia da carta, publicada pelo P. Iriarte no Gregorianum. É anônima ou, melhor, esconde o nome sob o pseudônimo de Carnéades. Mas não há dúvida ser ela de Sanches: basta, para isso, olhar um pouco para a letra, papel, estilo, para certas excentricidades que aparecem, aqui e ali, muito próprias do nosso filósofo, e para certos pontos de contato com o Quod nihil scitur.
Esta carta deve ter sido escrita, segundo nota o P. Iriarte, por volta dos anos de 1589-1590, pois Sanches serve-se da segunda edição da obra do P. Clávio, In Euclidis... de 1589.
Resumo: (1-2) Confessa a sua desilusão de encontrar a verdade na física e na metafísica, e por isso acolhe-se à matemática. (3-4) Nem a geometria, nem a astronomia merecem o nome de ciências, por demasiado empíricas. (5-7) Na geometria, mesmo quanto aos princípios, há muitas flutuações e disputas. (8) Assunto da consulta: Proclo, na 14 prop. do liv. I. (9) Desculpa-se de o vir incomodar, mas confessa-lhe que a sua primeira resposta o não satisfez. (10-12) Conveniência em simplificar as provas. (12-16) Inconsistência da resposta dada, com exemplos e discussão. (17) Não pretende impugnar Euclides. (18) Deseja ser ensinado e corrigido; despedida afetuosa.
***
Uma carta de Francisco Sanches a Cristóvão Clávio
+
Ao sapientíssimo e piíssimo varão, o senhor
Cristóvão Clávio [1], Carnéades, filósofo: saúde!
(1) Perante o desespero que, de há muito, se apoderou de mim, de poder descobrir e conhecer a verdade, no tocante às coisas humanas, ilustríssimo senhor, o que me tem acarretado inúmeros trabalhos, tomei muitas vezes a resolução de não me importar mais, nem de combater tantos erros que povoam a terra e que me fazem andar a braços com tantos desgostos, dos quais outro fruto não colhi, que levar uma vida miserável. E sendo a verdade uma só, reta como uma linha, e inúmeros os erros, como uma oblíqua, a maior parte dos homens deixa-se levar do erro, nem pode ser de outra maneira. Não acabo, contudo, de me resignar a esquecer o meu propósito, e milhares de vezes saio da minha trincheira, a ver se consigo descobrir, algures escondida, a verdade. Esforço vão! Que fazer? Deus deu ao homem este triste emprego, como diz o sábio, para que nele se ocupasse! [2]
(2) Buscando eu, outrora, a verdade através da Física e da Metafísica, sem jamais a poder descortinar, alguém me disse ter ela estabelecido o seu pouso entre as coisas naturais e as transnaturais, isto é, na Matemática. Ávida e alegremente acorro; e como o general avisado, ainda que veja as portas da cidade inimiga abertas, não entra temerariamente nela, mas, temendo insídias, manda adiante exploradores, para que tudo sondem e examinem e, ao atacar de surpresa uma província hostil, não deixa, atrás de si, nenhuma defesa ou fortaleza do inimigo, que não destrua e aplane, assim eu, logo ao pôr os pés no átrio das Matemáticas, hesitei, temendo, de todos os lados, desconfiado e suspeito, o dolo. As vantagens foram palpáveis. Sem essa desconfiança, teria caído em terreno minado, qual é o que se cava no campo da Matemática, não tão grande e vasto como no da Física e da Metafísica, mas por isso mesmo mais difícil e perigoso.
(3) Não vou discutir, presentemente, se as disciplinas matemáticas se devem contar entre as demais ciências, o que não ousaria afirmar, pois dependem mais dos sentidos que da razão e, por isso, são mais certas, se algo de certo existe neste mundo. De feito, a verdadeira ciência pretende conhecer, antes de mais, a Deus, depois a Natureza, sua escrava, interna e externamente, ou, no dizer de Aristóteles, conhecer as coisas pelas suas causas. Ora, comparar lado com lado, ângulo com ângulo, figura com figura, o todo com as partes, proporções com proporções, inscrever figuras umas nas outras, investigar finalmente as demais propriedades de ambas as quantidades, pode denotar engenho e agudeza; não é, no entanto, científico.
(4) No que diz respeito, por exemplo, à Astronomia, aumentastes os círculos concêntricos, excêntricos, epiciclos; tecestes ótimas teorias, como sempre o pensamos, sobre a trepidação, número dos céus, que se multiplicam com toda a facilidade, e outras coisas semelhantes, necessárias, sem dúvida, úteis à observação e indicação dos fenômenos, e à conservação da economia eclesiástica. Tudo isto, ótima e firmemente, como vós mesmo o afirmais, procurou corrigir Copérnico, admitindo que a terra era móvel e os céus imóveis, mas partindo de um falso suposto. Nem foge à tua perspicácia, a que nada escapa, quão frívola seja a sagacidade e engenho daqueles que dividem o céu em compartimentos e, contemplando o aspecto dos planetas e astros, atiram o pobre Nero para as pontas do punhal, logo no primeiro momento do nascimento: tão longe vão o furor e a temeridade do engenho humano!
(5) Mas voltemos à Geometria, que deve ser certíssima, pois se serve da régua e do compasso. Há nela, no entanto, muitas fendas, como se vai ver. Não bastam, em repetidos casos, os sentidos. Quando estes falham, recorre-se à inteligência. Ambos, por vezes, quer juntos quer separados, se enganam, sobretudo a razão. Muito me tem servido em tudo o bom senso, ainda desprovido, não digo de razão, mas de qualquer argumento, prova ou demonstração. Há muito de duvidoso na Matemática, não só nos princípios, mas também nos seus desenvolvimentos. Supõe, antes de mais, pontos, duvidando-se se e como existem, e também linhas e superfícies: aqueles, totalmente indivisíveis; as linhas, dividindo-se segundo o comprimento, as superfícies segundo a largura. Admite, por outro lado, como certas, outras coisas, como algumas definições, por exemplo, a de ângulo (na qual não concordais com Peletário [3]; e até nós duvidaremos dela, um dia), e a de proporções (sobre esta discordais vós de Orôncio [4] e de Peletário), bem como de algumas proposições, qual a décima terceira do livro I de Euclides, que vós, com Gémino [5] e Proclo [6], afirmais não pertencer ao número dos axiomas (Proclo, no entanto, ao querer prová-lo, comete uma petição de princípio, como vos julgais, e é mais obscura, aqui e ali, a prova, que o que se pretende provar), e a décima quarta, que o mesmo Proclo demonstra contra a natureza do princípio; enfim, muitas outras coisas, que por brevidade omito, que são obscuras e se prestam a discussão. Parece que, de novo, se admite uma quantidade contínua e indivisível, o ângulo de contingência, contra o que Aristóteles parece e crê ter demonstrado. Mas disto, se me derdes licença, trataremos noutra ocasião.
(6) Sabeis que Aristóteles foi ótimo matemático e conheceu o ângulo de contingência. Conclusão: os matemáticos vêem-se seriamente embaraçados, porque os seus princípios e regras não concordam, com o que se ensina, ao tratar das coisas naturais; e ainda que concordassem, nem por isso seriam mais certos, pois muito do que se ensina, a respeito das coisas naturais, é duvidoso e discutível.
Por fim, há muitos outros problemas, dos quais se duvida com motivo; se não aplicamos com todo o cuidado a força da razão, bastas vezes não atingiremos a meta, ainda mesmo apoiando-nos em demonstrações, como bem o mostrais a Peletário, homem aliás tão douto, a propósito do ângulo de contingência, ou ainda a este mesmo e a Orôncio, a respeito da definição e natureza da proporção. Vedes, pois, quanta perturbação acarreta consigo a ambigüidade de um só teorema: se estremece, virá a terra tudo o que nele se apoia. Tanto importa olhar, bem fundo, aos alicerces do edifício, não aconteça que este, como se dá com um mau pedreiro, apenas acabado de construir, venha a terra.
(7) Vede quão grande seja a miséria humana, e como esta se conjuga, por vezes, com a boa sorte! Acontece, com efeito, erguer-se, mesmo sobre débeis alicerces, o edifício que se pedia; não raro, também, a ciência progride, partindo de princípios absurdos ou obscuros. É o que se dá, precisamente, nos que edificam no mar ou em lugares pantanosos. Arremessam, ao acaso, enormes blocos até à superfície das águas, para de seguida construírem o que pretendem, segundo as regras da arte: assim, também, a Astrologia, de falsas suposições (que há aí de mais falso do que tantos, tão grandes e tais círculos, epiciclos, e inventar tudo o mais ao próprio sabor, idear os céus imóveis, e a terra móvel, crer que toda a terra e todos os mares formam uma esfera, equivalente a um ponto: tudo isto são princípios astrológicos) consegue acertar com as razões dos eclipses e demais coisas celestes. A Aritmética, igualmente, de uma regra, que os Árabes chamam Catain, e nós do Falso [7], deduz o que pretende; do mesmo modo, o dialético, de premissas falsas, conclui, com admirável lógica, por vezes, a verdade; e, finalmente, vós próprio que por meio da linha quadradora, engenhosamente lançada, pondo de parte apenas alguns detalhes, ensinais a realizar a quadratura do círculo. Disse que a Astrologia deduz, com bastante verdade, o que pretende: conheceis, sem dúvida, quanto se tem trabalhado, ultimamente, na reforma do Calendário, onde haverá sempre que melhorar.
(8) Mas já muito faz o homem com pretender aproximar-se da verdade. Eu, quanto está da minha parte, examino tudo, cuidadosa e escrupulosamente, para me ajustar com ela, afastando-me o menos possível [8]. Ora, examinando, um dia, nos vossos doutíssimos e substanciosos comentários a Euclides, a prova de Proclo à décima quarta proposição do livro I, e que há bem pouco vos enviei, pareceu-me que Proclo se enganara no seu raciocínio. Não quero, com isto, menoscabar, por pouco que seja, a estima daquele varão sapientíssimo, e menos ainda a vossa, pois estais acima de toda a crítica ou inveja; o facto, porém, só virá aumentar o vosso renome. Costumam os flecheiros arremessar as seus dardos para o alto, e sucede, convosco e conosco, vós magnates e nós desprezíveis, o que se passa com ricos e pobres. Mais facilmente se anicha certa negligência ou esquecimento nos cantos da casa do príncipe do que aparece no casebre do pobre e, enquanto o rico progride às mãos cheias, o miserável corre atrás de um tostão.
(9) Por isso, não me julguei, por então, bastante digno; passaram já muitos anos, para vos importunar com semelhantes ninharias, pois sabia terdes, entre mãos, importantíssimas questões. Mas sempre venceu o amor da verdade, e a oportunidade. de certo mensageiro, ou até, como sói dizer-se, o influxo não sei de que constelação, ou melhor, um conjunto de circunstâncias, levaram-me a molestar-vos agora, contando já fazê-lo, ainda outra vez, mais tarde. Esta, a desgraça dos grandes homens: serem importunados e perseguidos pelos pequenos, como Hércules pelos pigmeus. Não vos admireis, portanto, ilustríssimo senhor, se eu, um desconhecido de vós e de todos, na ciência e na realidade, vos venha, mais uma vez, interromper, um tanto, nos vossos importantíssimos estudos. Estou certo de que o fareis de boa vontade, dada a virtude que nos atraiu a vós, e a caridade a que vos consagrastes totalmente; concedei-me mais, ainda, este benefício, pois só é tal, quando não espera retribuição, tanto mais que é próprio da vossa religião [9] ou, melhor, de toda a sociedade humana, ligar os homens entre si por meio de obséquios. Respondestes, pois, às dúvidas que se me apresentaram ao espírito contra Proclo, argutamente e em poucas palavras; mais, no entanto, do que esperava. Julgava, eu, ter demonstrado tão claramente o que pretendia, que me persuadi ser impossível, caso não me tivesse enganado, dar-se-me qualquer resposta cabal, e se aquela demonstração fosse de Euclides, desesperaria, de vez, de alcançar a certeza em Geometria, ainda que não confio muito nela, como terei talvez ocasião de o mostrar, mais tarde. Vós, com todo o vosso engenho e sinceridade, procurastes defender o exímio Proclo. Contudo, a vossa douta resposta, não só me não arrancou o escrúpulo, como mais me confirmou nele. Vou, pois, expor a minha opinião sobre isso, em poucas palavras.
(10) Concedeis-me, primeiro, que Proclo podia, como eu afirmo e provo, demonstrar a sua tese com menos palavras, como vós provastes, bem mais brevemente do que Euclides, muitas das suas proposições. Mas, acrescentais logo, isso não é defeito. Eu julgo o contrário, apoiando-me na opinião geral, de que em vão se diz, em longo arrazoado, o que se pode exprimir em poucas palavras; e que é grandíssimo defeito, num mestre, explicar qualquer assunto com grandes discursos, mas confusos, podendo-o fazer claramente em poucas palavras, sobretudo na Matemática, onde, quanto for possível, nós devemos estribar nos sentidos. Por tal motivo, louvo-vos grandemente, porque sabeis ensinar muitas coisas com método e facilidade, nem concordo com o douto Peletário que criticava o aproximar figura a figura, corpo a corpo, ao querer comprovar a mútua igualdade ou desigualdade, como reza o oitavo axioma do livro de Euclides. A minha opinião é, exatamente, a contrária: tudo o que podermos conseguir a olho com o compasso e régua, devemo-lo fazer, sem nos metermos no caminho longo da demonstração, senão no caso dos sentidos falharem; tão avesso sou a grandes, longos e difíceis raciocínios que, por vezes, só tornam mais escuro o que, de si, é claro!
 |
| Figura 1 |
(11) Se tivesse de construir um triângulo equilátero sobre determinada linha AB, contentar-me-ia com abrir o compasso e, medido o comprimento da linha dada, colocá-lo-ia de A a B e de B a C (o mesmo se poderá fazer para a outra parte da linha) e de C a A, até encontrar o ângulo ACB, e uma vez encontrado, o que é facílimo, de um só golpe traçaria o triângulo, sem ter que provar tratar-se de triângulo equilátero, pois o compasso o manifestaria, sendo muito mais fácil acreditar na medida dos três lados, do que na confecção de dois círculos primeiro, para depois traçar os lados.
 |
| Figura 2 |
Do mesmo modo, se tivesse de dividir um ângulo reto, em duas partes iguais, operação que vós ensinais a fazer mais facilmente do que Euclides, traçaria duas linhas iguais AB e AC, e depois a reta AD, que daria origem a dois ângulos absolutamente iguais, provando, deste modo, o que pretende o 8 axioma do livro I, e a 4, 5 e 8 proposições do mesmo, muito mais facilmente do que o faz Euclides no 9 do livro I. Sentimos, contudo, prazer na dificuldade e andamos à cata de desvios, para que nos não taxem de empiristas ou pouco versados na matéria, pretendendo mostrar, pela razão, o que é patente aos sentidos, invertendo assim a ordem das coisas. Muito teria que dizer a tal respeito, o que omito, agora, por brevidade, esperando escrever, sobre isso, em tempo mais oportuno.
(12). Mas, como dizíamos, pouca importância teria o que apontamos, se a prova de Proclo fosse verdadeira. Não o é; ao contrário, é capciosa, como provávamos, quando afirma serem os ângulos ACF e ACE iguais a dois retos.
 |
| Figura 3 |
Respondeis-me, vós, que tais ângulos se devem tomar separadamente, não enquanto um é parte do outro, pois só desta maneira poderão igualar dois retos. Ainda que, na minha escaramuça passada, preveni esta resposta, parecendo-me tê-la refutado suficientemente, de novo volto a ela, para o mostrar mais claramente. Se eu afirmasse que o sapientíssimo Clávio, com a sua cabeça, é Jano de duas caras, haveria alguém que me acreditasse? Suponhamos que tínhamos, ambos, o mesmo pai, e que vos legara, por testamento, duas geiras de terra, equivalentes, digamos, a outros tantos ângulos retos, e a mim me constituíra herdeiro. Ficaríeis satisfeito, se vos desse, apenas, uma medida de terra, equivalente ao ângulo ACF, que na demonstração de Proclo iguala dois ângulos retos? Ora é precisamente disto que tratamos, pois a questão versa sobre Geometria, ou seja, sobre a medida da terra. Se vos vendesse duas geiras de terra por 2.000 dinheiros, sejam estes, como fizemos acima, os dois ângulos retos, ficaríeis contente com os dois ângulos traçados por Proclo? Não de certo; pelo menos, o meu caseiro não aceitaria, por mais que insistísseis na prova. E se, tendo-me emprestado 20, eu vos restituísse apenas 15, apoiando-me neste raciocínio: 15, mais os 5 neles incluídos, igualam 20; ora dou-vos 15; logo, paguei-vos o que devia, admitiríeis semelhante conclusão? E, se quisésseis comprar em qualquer loja, uma certa medida de pano para vestido, seja AB, e vos dessem apenas CD, acrescendo que CD + CE equivalem a AB, não seria demasiado curto o vosso vestido? Não se oculta, em tudo isto, um sofisma?
 |
| Figura 4 |
E, se a Matemática procedesse em tudo, assim, não seria apenas uma disciplina enganadora? Se ACF equivale a ACD + BCD, que haveríamos de dizer do enunciado 9, tão certo: o todo é maior que a sua parte?
 |
| Figura 5 |
(13) Mas, dir-me-eis: o ângulo ACE deve-se tomar separadamente, não enquanto faz parte do ângulo ACF. Mas tal resposta envolve uma contradição, como se dissésseis que se devia tomar a parte não-parte, o homem não-homem. Se eu vos imaginasse distinto do sapientíssimo Clávio, pensaria bem? E, se vos tivesse na conta de ignorante, não seria eu um louco? E, se tirasse ao vosso nome uma letra, bem insignificante e simples, Clávio não se converteria em cravo [10]? Pergunto: quando afirmais que o ângulo ACF equivale a um reto e meio, não compreendeis toda a quantidade contida entre as duas retas AC e CF? Logo, também os ângulos ACE, ECD, DCF, que são partes dela, e todos os demais ângulos que quiserdes traçar nesse espaço. Ora, quando de novo ajuntais ou tomais separadamente o ângulo ACE, onde o ides buscar? Será necessário pô-lo à vossa custa: eu não o consentirei à minha, e muito menos o ângulo ACF à sua.
(14) Mas já nos demoramos demais, numa coisa tão fácil e evidente. E, se isto acontece na lenha verde, que sucederá na seca? i. é, se tanto suamos em provar um problema tão fácil e manifesto, que acontecerá nos mais difíceis e obscuros? Acrescentais, depois, na vossa resposta, que os dois ângulos se devem tomar a seguir. Sabeis que a palavra ἐφεξῆς (a seguir, usada aqui por Euclides, tem, em Aristóteles, outro sentido, querendo significar, não o lugar, mas a ordem. Por isso, preferiria traduzi-lο por: da outra parte, de modo a compreender as linhas BC e BD, que se encontram com o ponto extremo da linha AB, e as linhas EF, e FG, que cortam a mesma reta AB no ponto F. Em todo o caso, acho melhor a expressão: a seguir, do que a que emprega Campano: em volta de si; pois, as duas retas EF e FG fazem, em volta de si, com AB, quatro ângulos ou retos ou iguais a retos. Mas isto pouca importância tem.
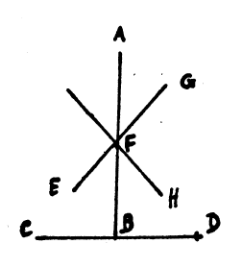 |
| Figura 6 |
(15) É certo que os dois ângulos se devem tomar da mesma parte da reta, transversal à outra. De outra maneira, como demonstrais claramente, ainda que as retas EF e FH façam com AB dois ângulos AFH e EFB, iguais a dois retos, não formam, contudo, uma só linha, porque o ângulo AFH deita para a parte A, e o outro EFB para a parte B. De passo, quero tirar argumento em favor da minha tese. Se o ângulo AFD (este tamanho lhe assinava Proclo), não basta para obter dois ângulos iguais a dois retos, ainda que o dividamos por meio de qualquer reta, devendo acrescentar-se-lhe ou EFB, como vós fazeis, ou AFC, ou BFD, para termos dois ângulos iguais a dois retos, segue-se evidentemente, que o ângulo AFD, ainda que se divida milhares de vezes, jamais igualará dois ângulos retos. Por fim, contra a minha demonstração, em que concluía, que se a prova de Proclo tinha algum valor, se seguiria dela que duas retas CF e FG seriam uma só linha continuada, já que constituíam dois ângulos CFG e CFA (os quais, segundo Proclo, são iguais a dois retos), tirados de um e de outro lado, originando ângulos seguidos, e contudo, como é evidente, não são uma só linha, contra isto, digo, como subtil artífice que sois, apresentastes ótimo subterfúgio e escapatória. Vale, talvez, no foro judicial; não, porém, no da consciência.
 |
| Figura 7 |
 |
| Figura 8 |
(16) Dizeis, de fato, que aqueles dois ângulos se não originam ambos em F (a vossa figura tem outras letras, mas vem a dar no mesmo), sobre a linha AB, pois AFC abre-se sobre a reta AB, mas não CFG. Logo, não se segue que CF e FG devam fazer uma linha. Mas a minha afirmação ou negação, como sabeis, não faz mudar as coisas. Mais: ainda que afirme algo contra aquilo que a coisa é ou não é, a proposição continuará a ser verdadeira ou falsa. Nem qualquer quantidade, de qualquer maneira que a olhardes, ou quaisquer que sejam as figuras ou linhas que lhe inscreverdes, aumentará ou diminuirá, por isso.
Assim, se dividirdes o trapézio ABCD com as retas AC e AE, originando, desse modo, três triângulos, não ficará, por isso, maior ou menor, e o mesmo acontecerá, se traçardes ainda a reta BF, que o dividirá em quatro ângulos e dois trapézios. Logo, quaisquer que sejam as linhas tiradas entre ACF (para, de novo, voltarmos à minha e vossa primeira figura), jamais conseguireis aumentar ou diminuir aquela quantidade. Podereis, sem dúvida, aumentar ou diminuir o número dos ângulos; nunca, porém, obtereis, que aquela quantidade valha mais ou menos que um ângulo reto e mais meio. Mas a quantidade do meu paralogismo (é, verdadeiramente, um paralogismo à imagem da argumentação de Proclo), GCD, é igual, em tudo, à quantidade do de Proclo, ACF. Ora, se a de Proclo equivale a dois ângulos rectos, também com a minha sucederá o mesmo. Nem é necessário, nem Euclides o afirma, que a linha AB se repita duas vezes, uma em cada ângulo, como vós quereis. Mas, concedamos que Proclo tivesse dito assim: o ângulo ACF equivale a um reto e meio, e o ângulo FCD a meio reto; logo, ambos os ângulos ACF e FCD igualam dois retos. Não seria o mesmo e não concluiria do mesmo modo, ainda que a linha AB se não repetisse no segundo ângulo? Logo, o geômetra deve atender à quantidade, não ao traçado de linhas, que outro fim não têm senão fazer-no-la apanhar, mas sem delas depender. Concluís, enfim, que jamais se poderá demonstrar algo contra Euclides, que não há tais paralogismos em Matemática, e que fui eu que me servi de paralogismos.
 |
| Figura 9 |
(17) Mas eu, por ora, nada quis demonstrar contra Euclides, antes só contra Proclo. Aquele, decerto, se hoje vivesse, não defenderia este, nem as suas obras o defendem, pois nelas nada se encontra que se pareça com esta demonstração ou paralogismo de Proclo. Se for necessário demonstrar algo contra Euclides, poderemos, talvez, fazê-lo, não num só lugar, mas em 2 proposições do livro III, e no ângulo de contingência, o qual, ao parecer, não pode ser menor que qualquer ângulo agudo retilíneo ou só em quantidade mínima, contra as afirmações de Aristóteles e do mesmo Euclides 1, décimo (livro). Nem, por isso, seria obrigado a aceitar o parecer de Peletário, homem aliás doutíssimo, que não admite nem tal ângulo, nem tal quantidade. Aos seus paralogismos, respondestes vós, sapientissimamente, dando-lhes tal nome; donde se colhe poderem dar-se, também, paralogismos em Matemática, para não falar de outros, a que se refere Pedro Nunes, grande autoridade em Matemática, no seu livro sobre Orôncio. Mas, se fòrdes de opinião que não se fazem paralogismos assim, e julgardes não ser tal a argumentação de Proclo, pouco me importa o nome, contanto que admitais que a sua prova é insubsistente.
(18) Concedo-vos, sim, que tenha eu usado de paralogismo. Só quis, neste ponto, imitar o paralogismo de Proclo, e consegui-o, se não me engano. Sabeis que, no arguir, muito aproveita mostrar a consequência absurda do adversário, mudando simplesmente a matéria e guardando a forma. Mas quero, concedo, afirmo, ter-me enganado; desejo ser ensinado e vencido; tenho, até, sumo prazer, em descobrir os erros. Pelo que, se alguma coisa tiverdes sobre tudo isto, ser-me-ia muito grato receber resposta vossa. Não procureis saber quem sou: sou, apenas, outro Carnéades, amicíssimo, não da glória vã, mas da verdade e de vós. Adeus. [11]
Notas:
[1] O P. Cristóvão Clávio S. J., alemão por nascimento, veio em 1503, com 17 anos de idade, para Coimbra, cursar, no Colégio das Artes, letras, filosofia e matemáticas, para as quais dava mostras de singular vocação. Em 1550, observou, nesta cidade, o eclipse total do sol, que ele próprio descreve no seu Comentário à Esfera de João de Sacro Bosco. Em 1561, já estava em Roma, onde, no ano seguinte, começou a ensinar matemática no Colégio Romano, com tanta aceitação que lhe mereceu o apelido de Euclides do seu tempo. Cfr. Franc, Rodrigues, A Formação Intelectual do Jesuíta, Porto, 1917, págs, 283-284. De 1569 a 1573, viajou Sanches pela Itália, demorando-se, sobretudo, em Roma, onde deve ter cursado os estudos superiores, e onde conheceu, tratou e talvez, até, foi discípulo de Clávio.
[2] Comparar com o Quod nihil scitur: «Quid igitur nos consumimus? Nescio, Sic fata ferunt. Dedit Deus filiis hominum occupationem hanc pessimam ut in ea occuparentur» (à margem; Ecclesiast. 1).
[3] Jacques Peletier, médico e literato francês, nascido em Mans, em 1517, e morto em Paris, em 1582. Escreveu várias obras sobre geometria.
[4] Orôncio Fine, matemático francês, nascido em 1494, morto em Paris em 1555. Entre outras, escreveu a seguinte obra: In sex priores libros Geometricorum Elementorum Euclidis.
[5] Gémino, astrônomo e geômetra grego, o qual viveu um século antes de Cristo.
[6] Proclo, filósofo grego, neoplatônico, nascido em Constantinopla, em 412; morto em 495, Escreveu, sobretudo, sobre filosofia, e também um comentário ao I livro dos Elementos, de Euclides.
[7] Regra Catain ou do Falso: «Quando proposita aliqua quaestione per numerum solvenda, ponimus quemcumque numerum, qui propositae quaestioni putatur satisfacturus, licet reipsa non satisfaciat, et cum ipso procedimus prout quaestio vult, tandemque quaestionem solvimus, verum ac desideratum numerum inveniendo. Vocatur passim Regula Falsi, non quod falsum doceat, sed quod plerumque ex numero falso verum invenire doceat», Cfr. Gregorianum. Roma, 1940, vol. XXI, pág. 431, nota 39.
[8] Relevamos esta e outras expressões de Sanches, que mostram, de alguma maneira, a sua atitude perante o angustioso problema da verdade. Não nega, de modo nenhum, a sua existência, e é por isso que lança mão de tudo para se aproximar dela, o mais possível, servindo-se, separada e conjuntamente, dos sentidos e da razão, pois, mesmo assim, não atingem por vezes a verdade (cf. n. 5); há princípios que estão fora de toda a dúvida, como «o todo é maior que a sua parte» (cf. n. 12, ao fim), e apesar da sua crítica ao silogismo, no Quod nihil scitur (págs. 9, 11... ed. de 1581), não teme usá-lo aqui (n. 12).
[9] «Societatis vestrae», refere-se à Companhia de Jesus, a que Clávio pertencia.
[10] O trocadilho só dá bem em latim, pois, suprimindo no nome Clavius o i, ficará clavus.
[11] Gregorianum, Roma, 1940, vol. XXI, págs. 422-443.
***
Leia mais: O Matemático Jesuíta Cristóvão Clávio.
Leia mais em COMECE POR AQUI: Conheça o Blog Summa Mathematicae
Curta nossa página no Facebook Summa Mathematicae. Nossa página no Instagram.





